Dans cet article, nous étudierons l’évolution de la vente de supercarburants auto et la vente de gazole (en kt : kilo-tonne). Pour chacune des séries, nous utiliserons les données mensuelles allant de janvier 1981 à novembre 2016 soit 35 années d’observations. Après un bref descriptif de nos différentes séries, nous utiliserons pour chacune des séries, une approche différente pour son analyse. La méthode de Buys-Ballot pour la série de supercarburants (échantillon 1) et la modélisation ARMA par la méthode de Box Jenkins pour la série de gazole (échantillon 2). Notre objectif étant d’obtenir des prévisions pour les 12 prochains mois. Nous utiliserons la totalité des données pour construire les différents modèles de prévisions.
Notre étude porte sur l’analyse de 2 jeux de données issues des statistiques relatives aux produits pétroliers, à leur approvisionnement et leur consommation en France, en kilo-tonne (kt) sur la période allant de janvier 1981 à novembre 2016. Ces données ont été calculées de manière mensuelle sur une durée de 35 ans. Le premier jeu de données (échantillon 1 que l’on notera par la suite E1) contient l’évolution de la Vente de supercarburant auto (en kt) et le second (échantillon 2 que l’on notera E2 ) contient l’évolution de la Vente de gazole (en kt).
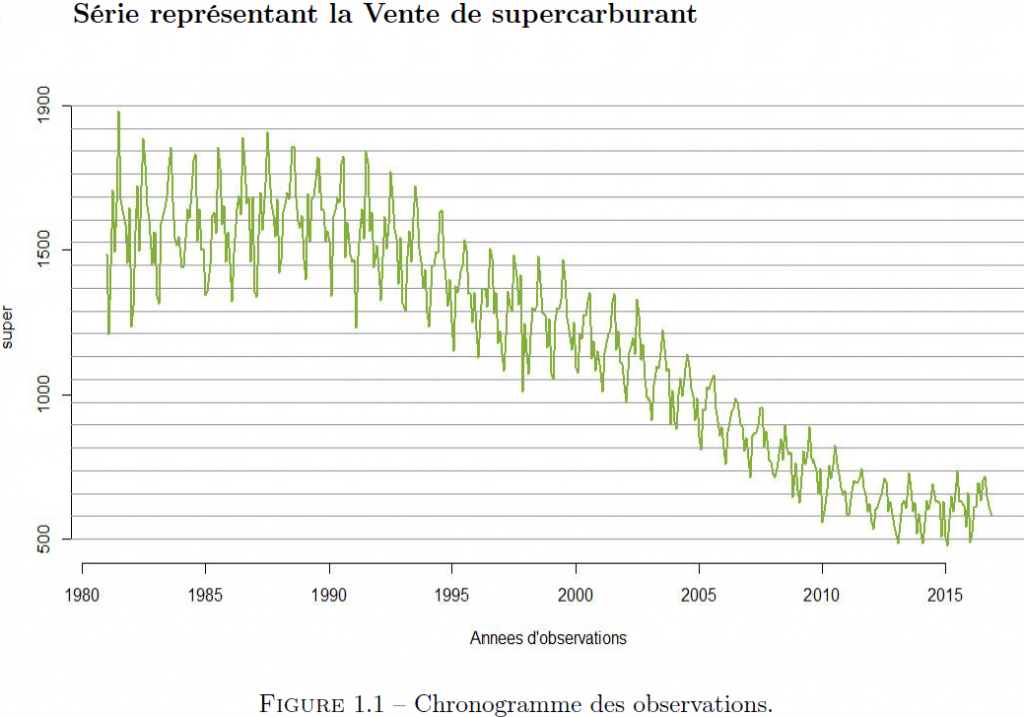
La représentation sous forme de série temporelle d’un jeu de données est utile dans la mesure où elle nous permet de mieux visualiser nos données, de détecter des valeurs atypiques, d’éventuelles ruptures ou un changement dans la dynamique de la série. En analysant la figure (1.1), nous pouvons dire que la vente de supercarburants auto a une évolution régulière en dents de scie (présente des motifs répétitifs). Nous remarquons également que la moyenne des oscillations varie de façon décroissante et quadratique avec le temps, ce qui peut être une cause de non stationnarité de la série temporelle. Par ailleurs, l’amplitude des oscillations semble décroître avec le temps, ce qui peut être un problème pour le choix et la forme du modèle (multiplicatif ou additif). Pour cela, nous analyserons la série du logarithme des observations de cet échantillon.
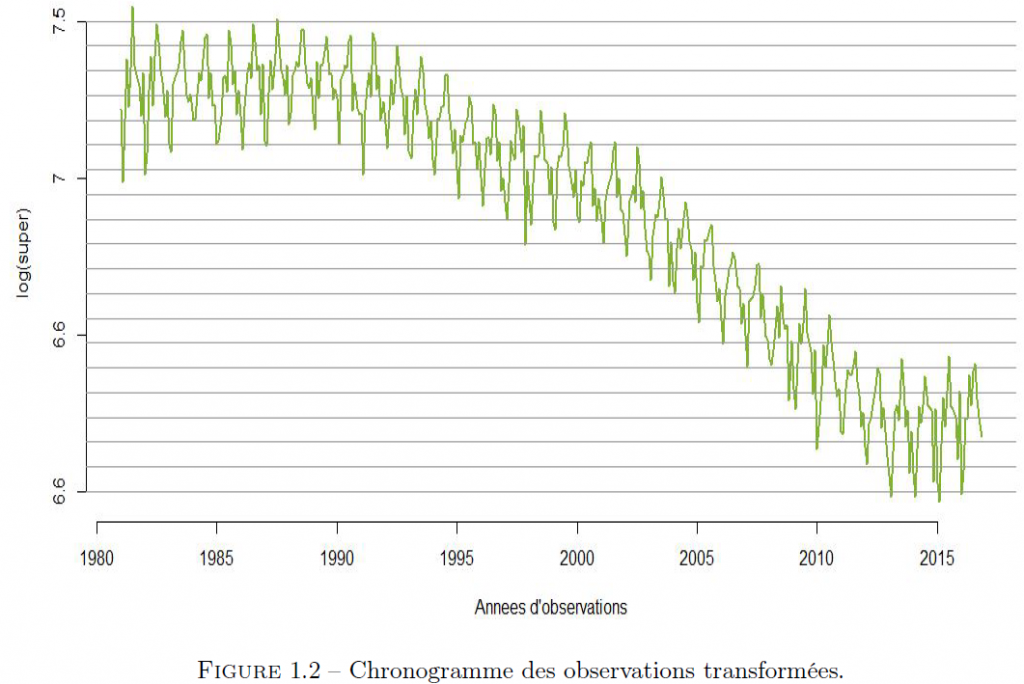
L’analyse de la figure (1.2) nous permet de tirer les conclusions suivantes : – La série logarithme de cet échantillon présente une saisonnalité mensuelle. – La série logarithme de cet échantillon présente une tendance quadratique (polynomiale). – Pour cet échantillon, on peut choisir un modèle additif, car les oscillations semblent varier entre 2 courbes parallèles. Dans la suite, nous ferons des tests statistiques afin de valider ou de réfuter ces affirmations.
Le diagramme retardé est un diagramme de dispersion des points ayant pour abscisse la série retardée de k instants et pour ordonnée la série non retardée. Il nous permet d’analyser la série par rapport à son passé.
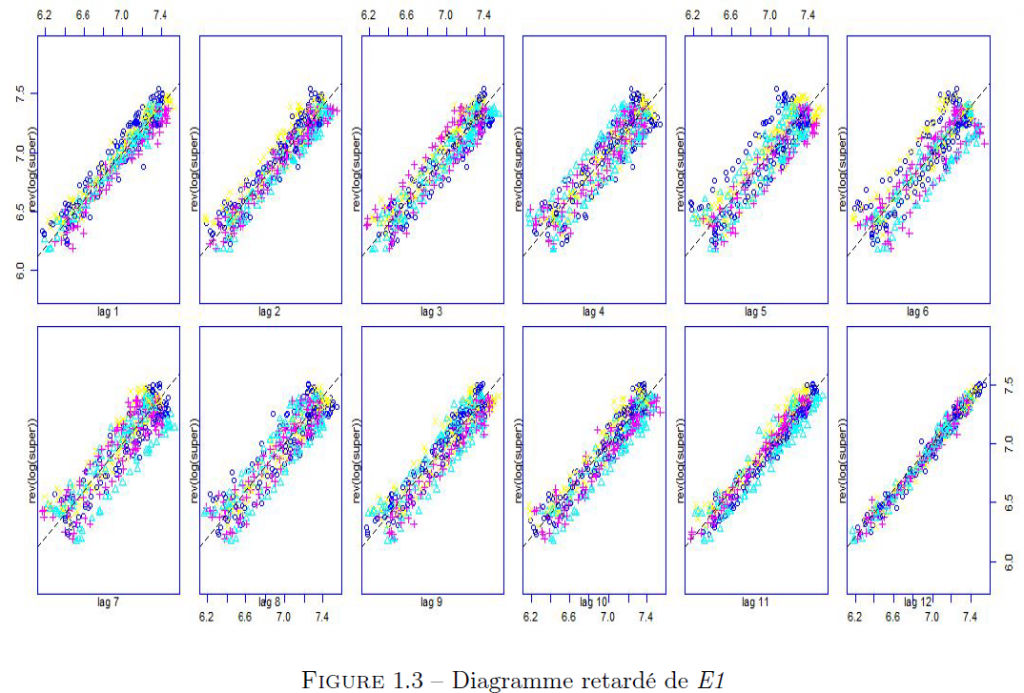
Nous remarquons que la forme allongée au retard 12 traduit une corrélation entre la série brute et la série décalée de 12 mois. Ce qui explique le fait que les valeurs de l’échantillon 1 d’un mois donné soient voisines d’une année à l’autre.
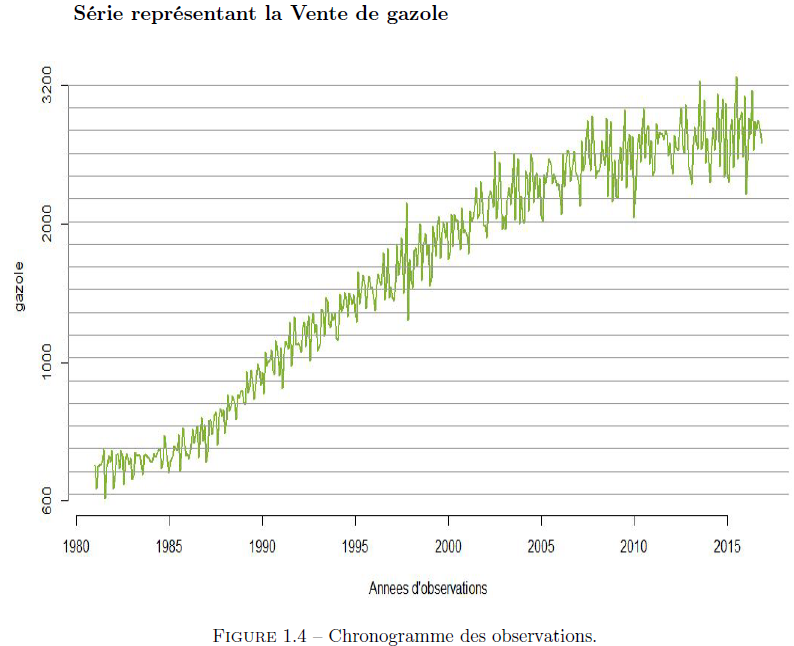
En analysant la figure (1.4), nous pouvons dire que la vente de gazole a une évolution régulière en dents de scie (présence d’un motif répétitif). Nous remarquons également que la moyenne des oscillations varie de façon croissante et quadratique avec le temps. Par ailleurs, l’amplitude des oscillations semble croître avec le temps, ce qui comme précédemment peut être un problème pour le choix et la forme du modèle (multiplicatif ou additif). Pour cela, nous analyserons aussi le logarithmique de la série des observations de cet échantillon.
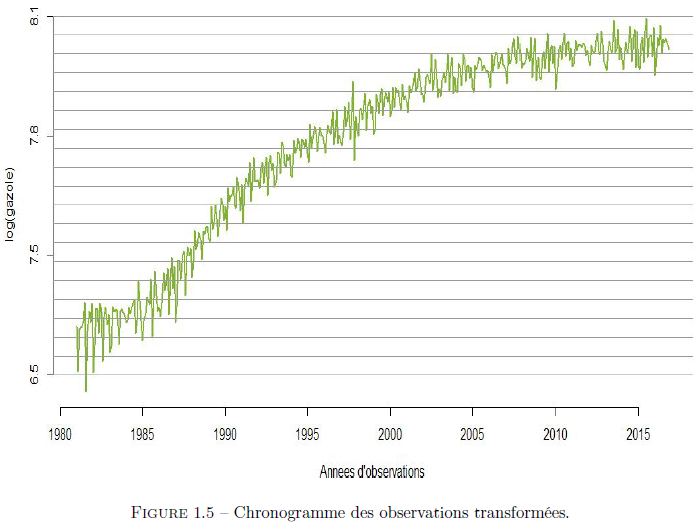
Au regard de la figure (1.5), nous pouvons donc dire que le chronogramme du logarithme des observations de la serie E2 présente : – Une saisonnalité mensuelle. – Une tendance polynomiale. – Pour cette série, on peut choisir un modèle additif car les oscillations semblent varier entre 2 courbes parallèles. De même, nous ferons aussi des tests statistiques afin de valider ou de réfuter ces affirmations.
Méthode statistique d’analyse des séries :
Dans cette partie, nous présenterons la démarche algorithmique nécessaire à la mise en oeuvre de 2 approches paramétriques : la méthode de Buys-Ballot et la méthode de Box-Jenkins (dans le cas où la chronique présente une tendance et une saisonnalité).
Application de la méthode de Buys-Ballot à l’échantillon 1 :
Le schéma additif retenu pour la décomposition de la série E1 dans le cas où la tendance est supposée polynomiale et les données mensuelles est équivalent au modèle (2.1) défini par : Xt = ln(E1t) = Tt + St + Yt (2.1) Où Tt est la tendance (polynomiale), St est la composante saisonnière (sous condition que la somme des coefficients saisonniers soit nulle) et Yt est une perturbation aléatoire représentant les erreurs non systématiquement centrées, pouvant être captées par un processus stationnaire faible. Ainsi : – Nous estimerons la tendance et les coefficients saisonniers par un modèle linéaire. – Nous estimerons la perturbation aléatoire en calculant la série débarrassée de la tendance et de la saisonnalité. – Nous ferons un test de blancheur et stationnarité de cette perturbation aléatoire. – Si la perturbation aléatoire qui en découle n’est pas un bruit blanc, mais plutôt un processus stationnaire, nous le modéliserons par un modèle ARMA pour faire nos prévisions. Dans la suite de cet article, nous commencerons par vérifier la stationnarité de Yt obtenu à partir du processus initial débarrassé de la tendance et de la saisonnalité. Pour aboutir à nos fins, nous ferons successivement : – Un test de KPSS (H0 : “la variance des résidus du processus est nulle i.e le processus est stationnaire”). – Un test de DICKEY-FULLER et de PHILLIPS-PERRON (H0 : “le processus est au moins intégré d’ordre 1”). – Une fois la stationnarité vérifiée, nous sélectionnerons les ordres du processus: soit manuellement à travers l’examen de l’ACF et du PACF ou automatiquement à travers un critère de minimisation de l’erreur de prédiction : le BIC avec BIC(p , q) = ln(sigma) + 2(p + q) * ln(n) / n (2.2) n étant la taille de l’échantillon, sigma l’écart type, p et q étant les paramètres du modèle. Nous estimons ensuite les coefficients du modèle retenu par maximum de vraisemblance en vérifiant la significativité des coefficients obtenus. Ensuite nous vérifions la blancheur du résidu qui en découle avec le test de blancheur de Ljung-Box et de Box-Pierce. Le modèle obtenu et validé permet de faire des prévisions puis de réintégrer la tendance et la saisonnalité précédemment enlevées.
Application de la méthode de Box-Jenkins à l’échantillon 2 :
Le schéma additif précédemment retenu pour la décomposition de la série E2 dans le cas où la tendance est supposée polynomiale et les données mensuelle est équivalent au modèle (2.2) défini par : Xt = ln(E2(t)) = Tt + St + Yt (2.3) où Tt est la tendance (polynomiale), St la composante saisonnière (sous condition que la somme des coefficients saisonniers soit nulle) et Yt une perturbation aléatoire représentant les erreurs non systématiquement centrées, pouvant être capté par un processus stationnaire faible. Contrairement à l’approche précédente qui consiste à estimer les causes de non stationnarité, puis s’en débarrasser, la modélisation ARMA par la méthode de Box-Jenkins consiste à se séparer de la tendance et de la saisonnalité par différentiation à travers un filtre adéquat (on cherche le nombre de fois qu’il faut différencier la série pour obtenir une série stationnaire) afin d’obtenir un processus stationnaire.
Résultats et interprétations :
Nous avons utilisé les méthodes de Buys-Ballot et Box-Jenkins respectivement pour l’étude des nos 2 séries de données. Ces deux méthodes permettent de capter la tendance et la saisonnalité de chaque série puis de s’en séparer. La série résultante dans chacun des cas est ensuite modélisée comme un processus ARMA.

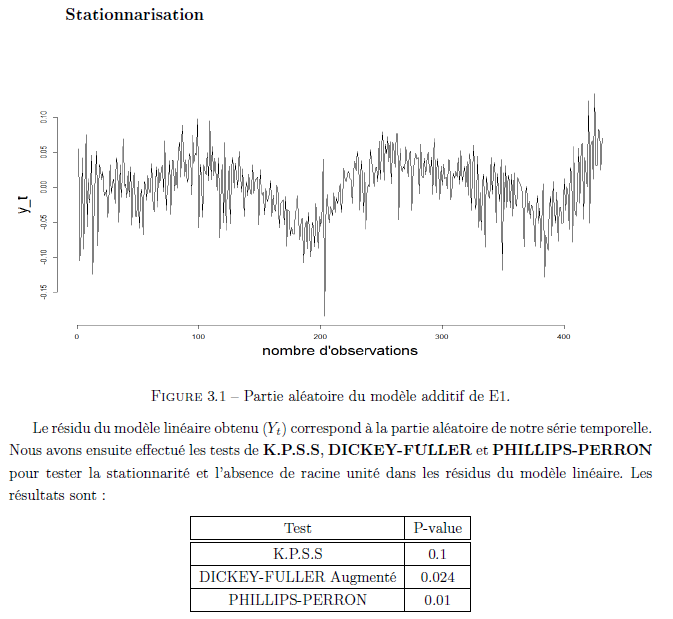
La valeur de la p-value du test de K.P.S.S (p-value > 0.05) nous fait ne pas rejeter l’hypo- thèse de stationnarité de la partie aléatoire de notre série temporelle. Avant de se lancer dans une modélisation ARMA de (Yt), nous testerons au préalable la blancheur de la série temporelle résiduelle à l’aide des tests de Llung-Box et Box-Pierce.

Modélisation :
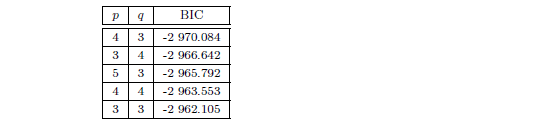
Dans cette partie, nous modélisons notre partie aléatoire comme un ARMA(p, q), p et q étant à déterminer. Afin de déterminer les ordres p et q, nous faisons une sélection automatique par minimisation du critère BIC et nous obtenons les résultats suivant :
Estimation :
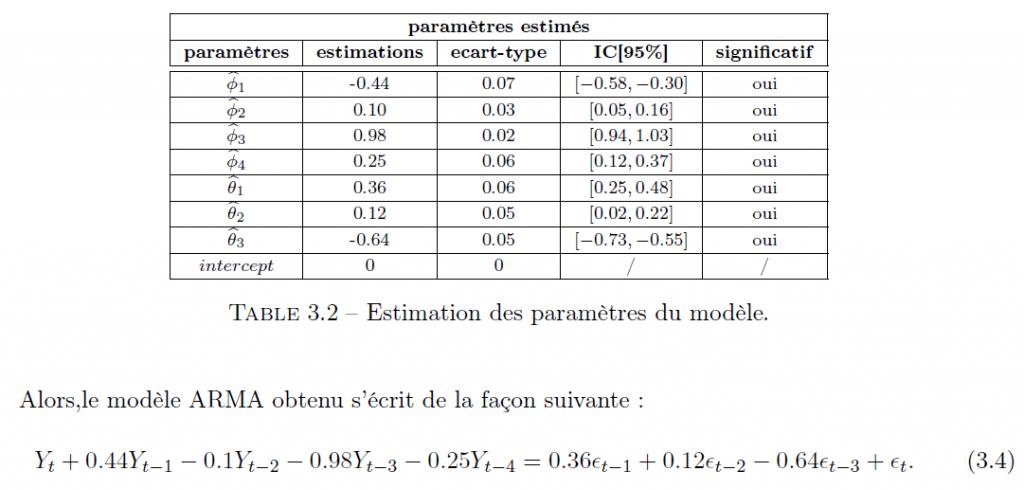
Au vue des résultats précédant, nous retenons le modèle ARMA(4, 3) pour modéliser la partie aléatoire (Yt) de notre modèle. Après estimation et vérification de la significativité des paramètres du modèle ARMA(4, 3), nous obtenons les estimations suivantes :
Validation du modèle :
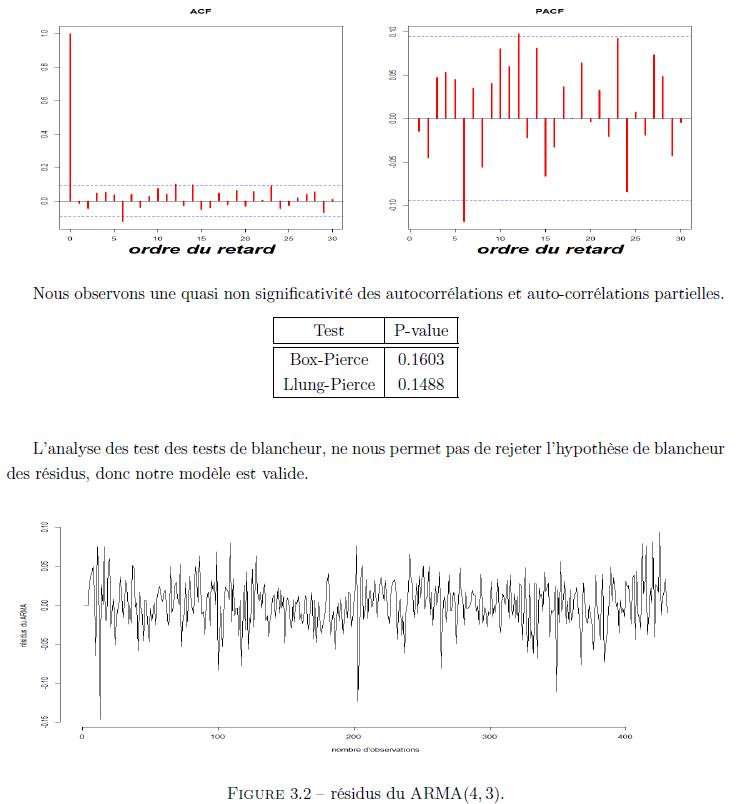
Afin de valider les hypothèse faites sur la forme de la partie aléatoire de notre série, nous vérifions la blancheur des résidus de notre modèle ARMA. Nous commençons par l’examen de l’ACF et du PACF des résidus du ARMA(4, 3).
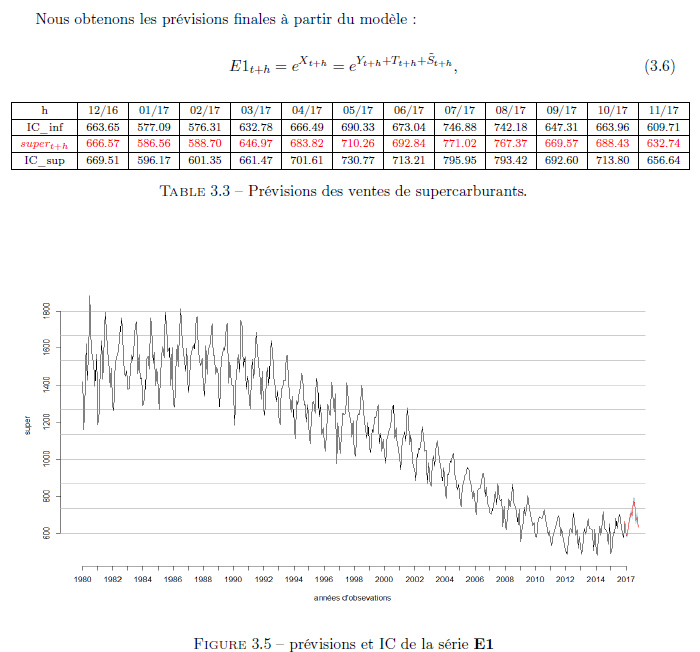
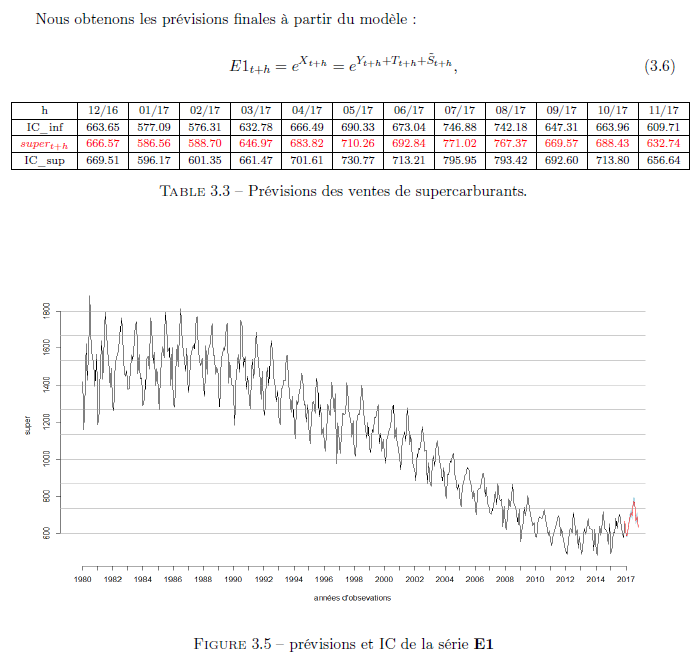
Prévision :
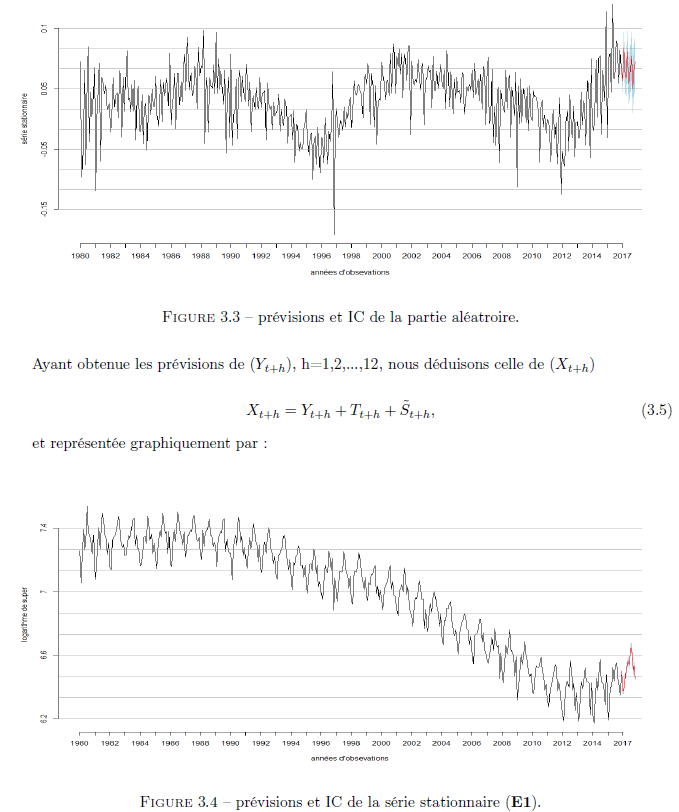
Nous commencerons par les prévisions avec le modèle ARMA pour les 12 prochains mois.
Méthode de Box-Jenkins :
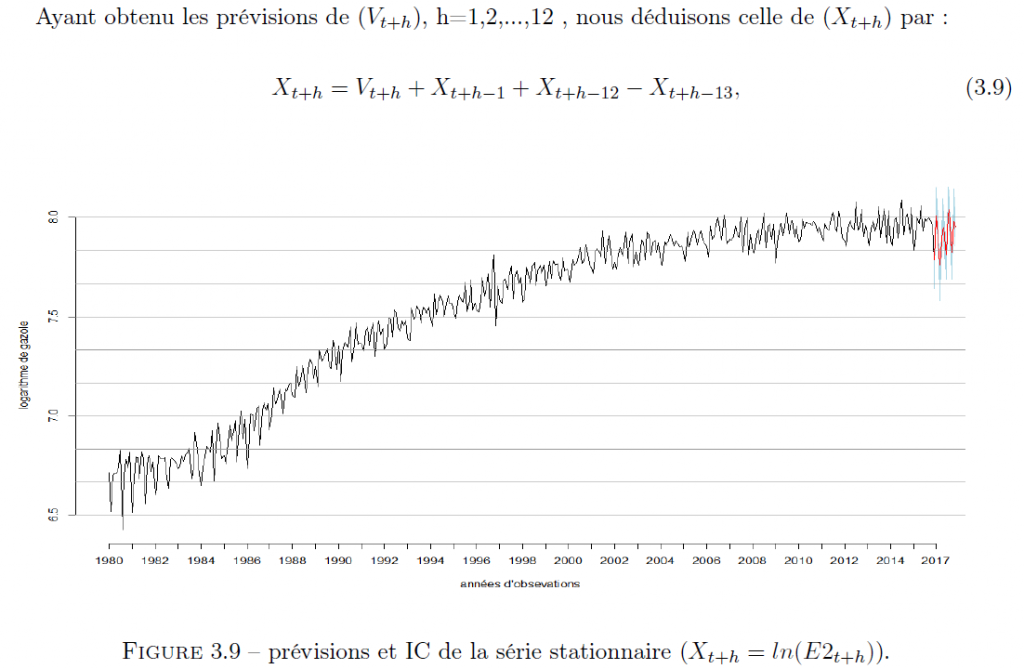
Stationnarité : Partant du modèle : Xt = ln(E2t) = Tt + St + Yt (3.7), nous commencerons par nous séparer de la saisonnalité à travers le filtre :
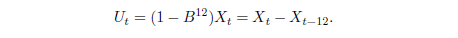
Nous effectuons donc des tests de stationnarité sur la série (Ut).

Nous rejetons l’hypothèse de stationnarité de la série (Ut) au vue des différentes p-value en particulier celle du test de KPSS (p-value < 0,05). La série n’étant pas stationnaire, nous la différencions à nouveau :
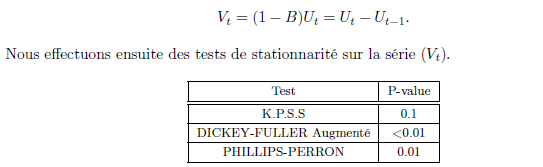
Au regard des différentes p-value, nous ne rejetons pas l’hypothèse de stationnarité de la série (Vt). La série obtenue après différenciation étant stationnaire, nous procédons à une modélisation ARMA.
Modélisation :
Nous allons modéliser notre série (Vt) comme un ARMA(p, q), p et q étant des paramètres à déterminer. Afin de déterminer les ordres p et q, nous examinons les ACF et PACF.
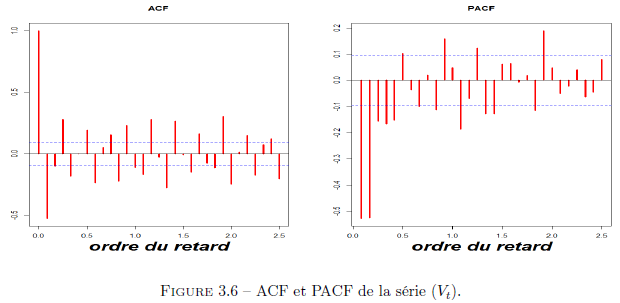
Après analyse des ACF et PACF, nous retenons p = 5 et q = 1. Nous confirmons cette première observation avec une sélection automatique par minimisation du critère BIC. Nos résultats sont renseignés dans le tableau ci-dessous :
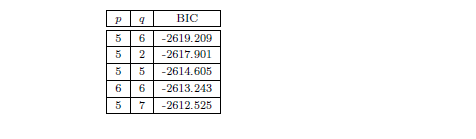
Estimation :
Afin de décider du choix des ordres de notre modèle, nous examinons les RMSE et MAE de notre série.
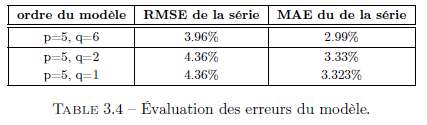
Nous retenons donc le modèle ARMA(5, 6) pour modéliser la série (Vt) de notre modèle. Après estimation et vérification de la significativité des paramètres du modèle ARMA(5, 6), nous obtenons les estimations suivantes :
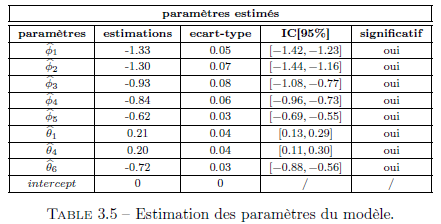
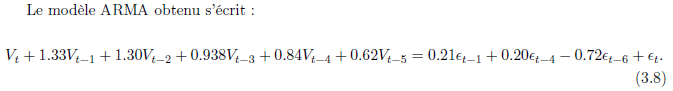
Validation du modèle :
Pour valider les hypothèses faites sur la forme de notre série, nous vérifions la blancheur des résidus de notre modèle ARMA. Nous commençons par l’examen de l’ACF et de la PACF des résidus du ARMA(5, 6).
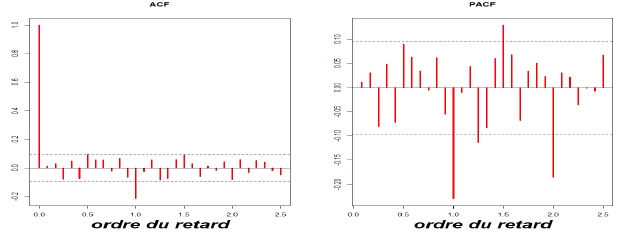
Nous observons une quasi non-significativité des auto-corrélations et auto-corrélations partielles. Vérifions cette première observation avec des tests de blancheurs :

Les tests de blancheurs ne nous permettent pas de rejeter l’hypothèse de blancheur des résidus i.e notre modèle est valide. Ci-dessous le graphe des résidus.
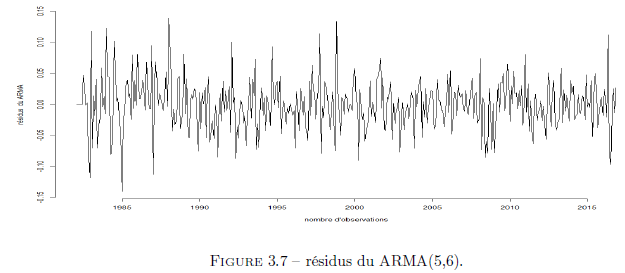
Prévision :
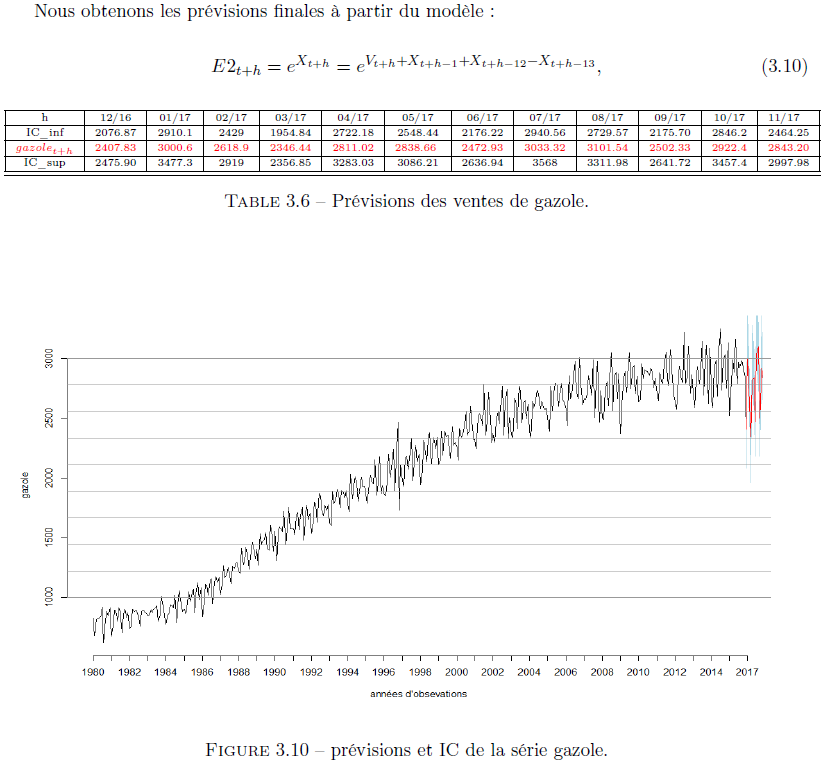
Nous commençons par les prévisions avec le modèle ARMA pour les 12 prochains mois.
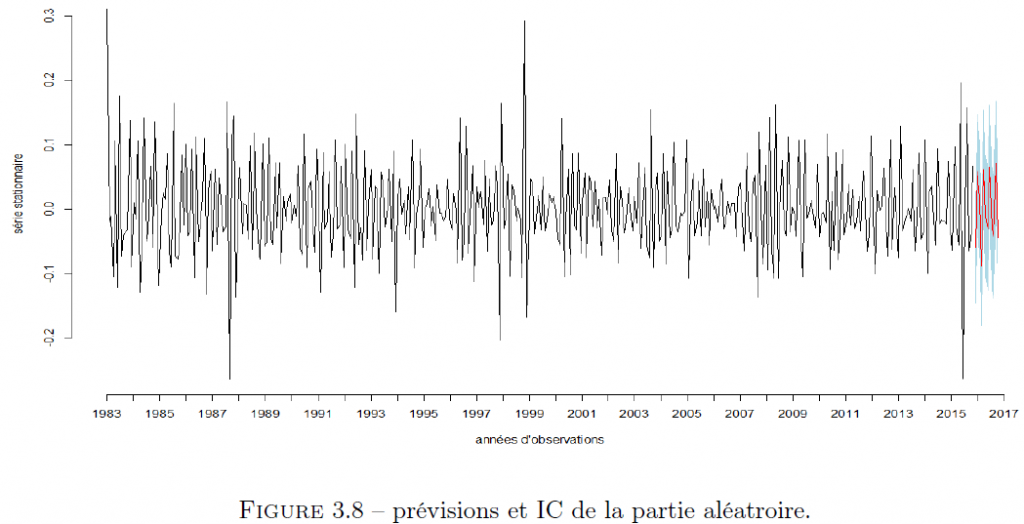
L’objectif de cet article était de prédire les valeurs des ventes de supercarburants et de vente de gazole pour les 12 prochains mois à partir des observations mensuelles sur 35 ans. Afin de valider nos modèles et de s’assurer que les valeurs trouvées étaient cohérentes, nous avons eu recours à des méthodes et tests statistiques adéquats. Les indicateurs de qualité tels que le RMSE et le MAE étaient pertinents (inférieures à 5%), ce qui nous a permis de valider la cohérence de notre modèle. Comme il est courant dans les problèmes d’estimations, on constate souvent des écarts entre les valeurs prédites et la réalité. Comment ajuster un modèle au cours du temps en fonction des valeurs réelles observées ?
Willie Lekeufack – Associé chez Cents Consulting